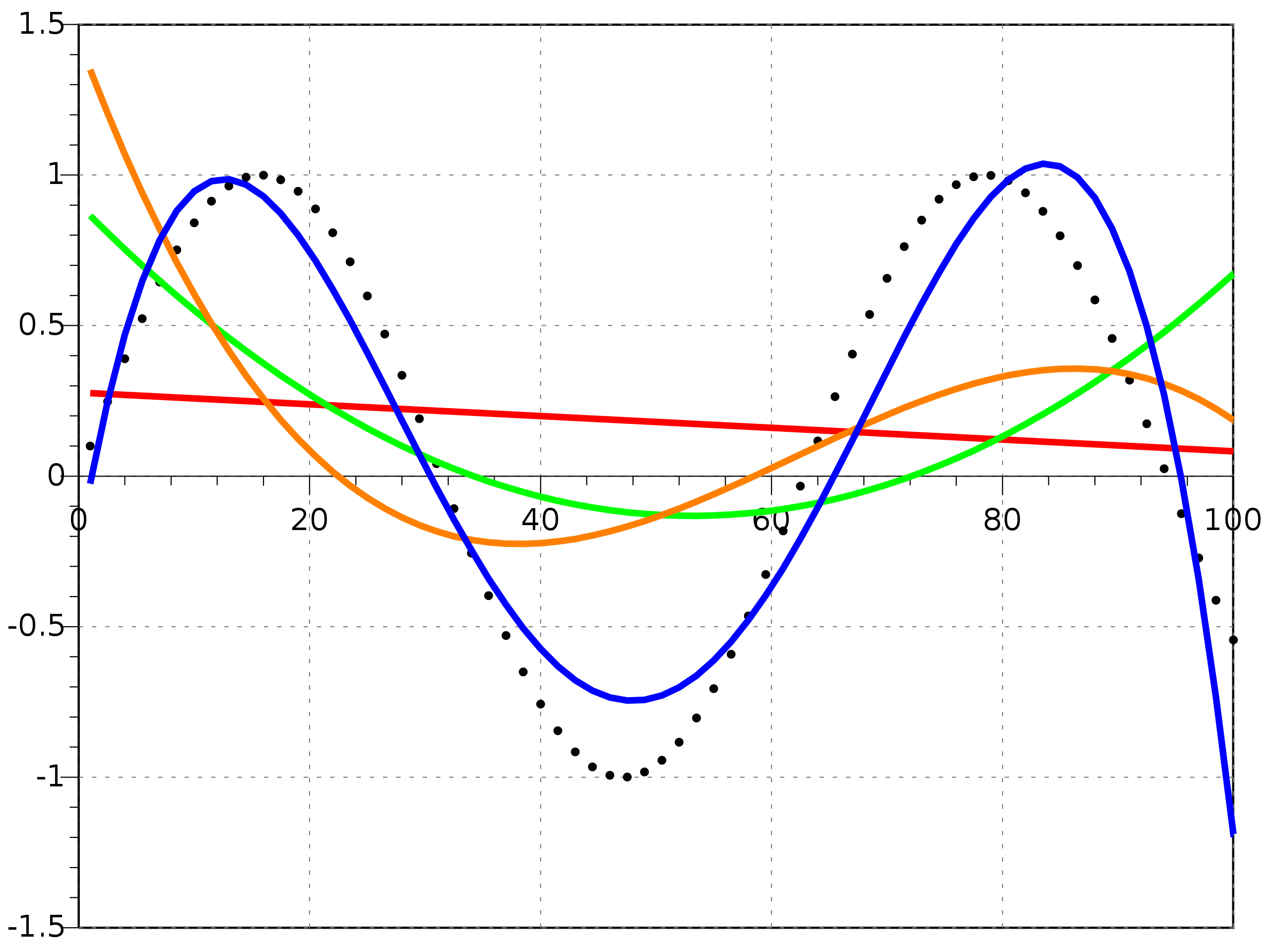
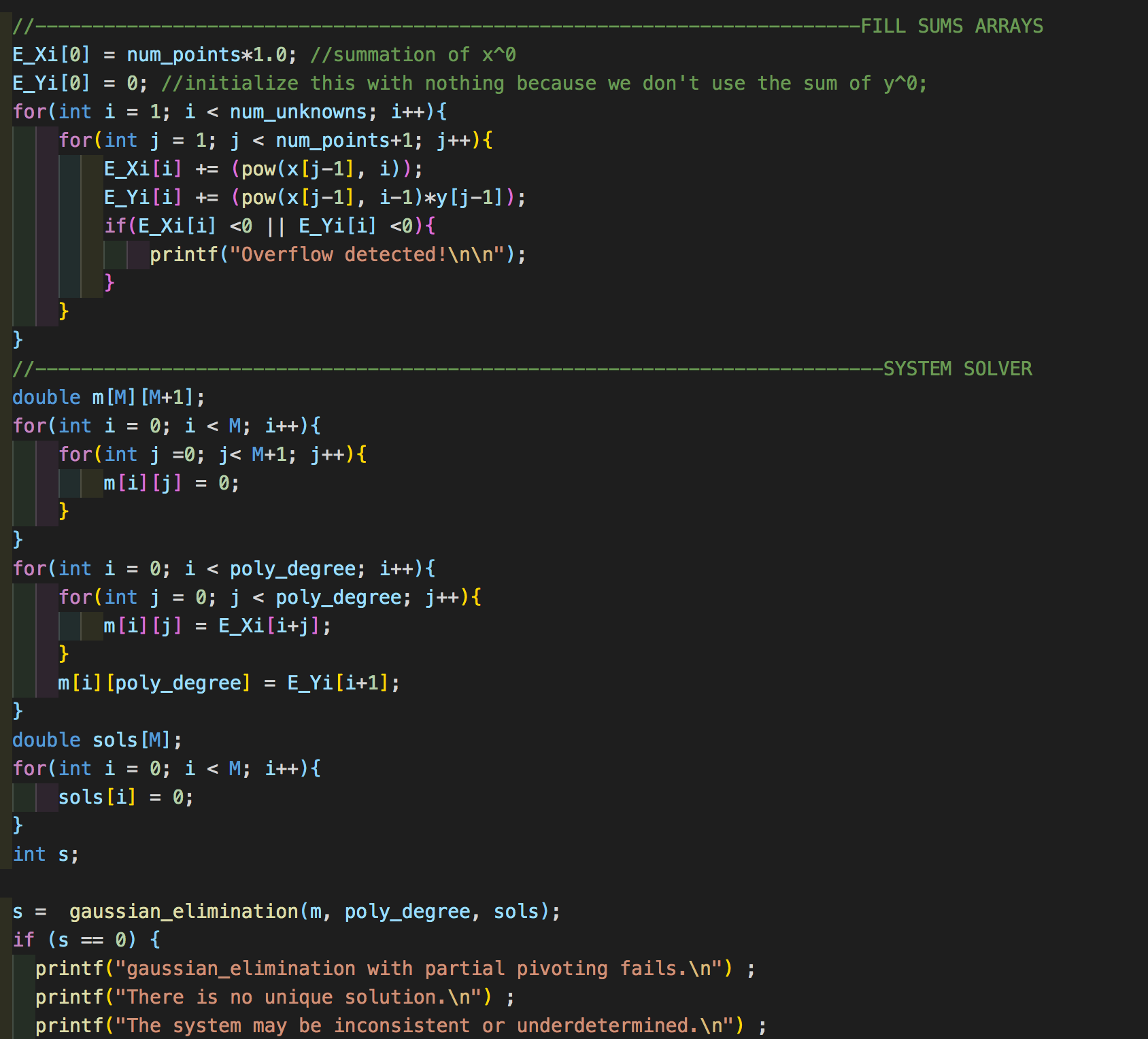
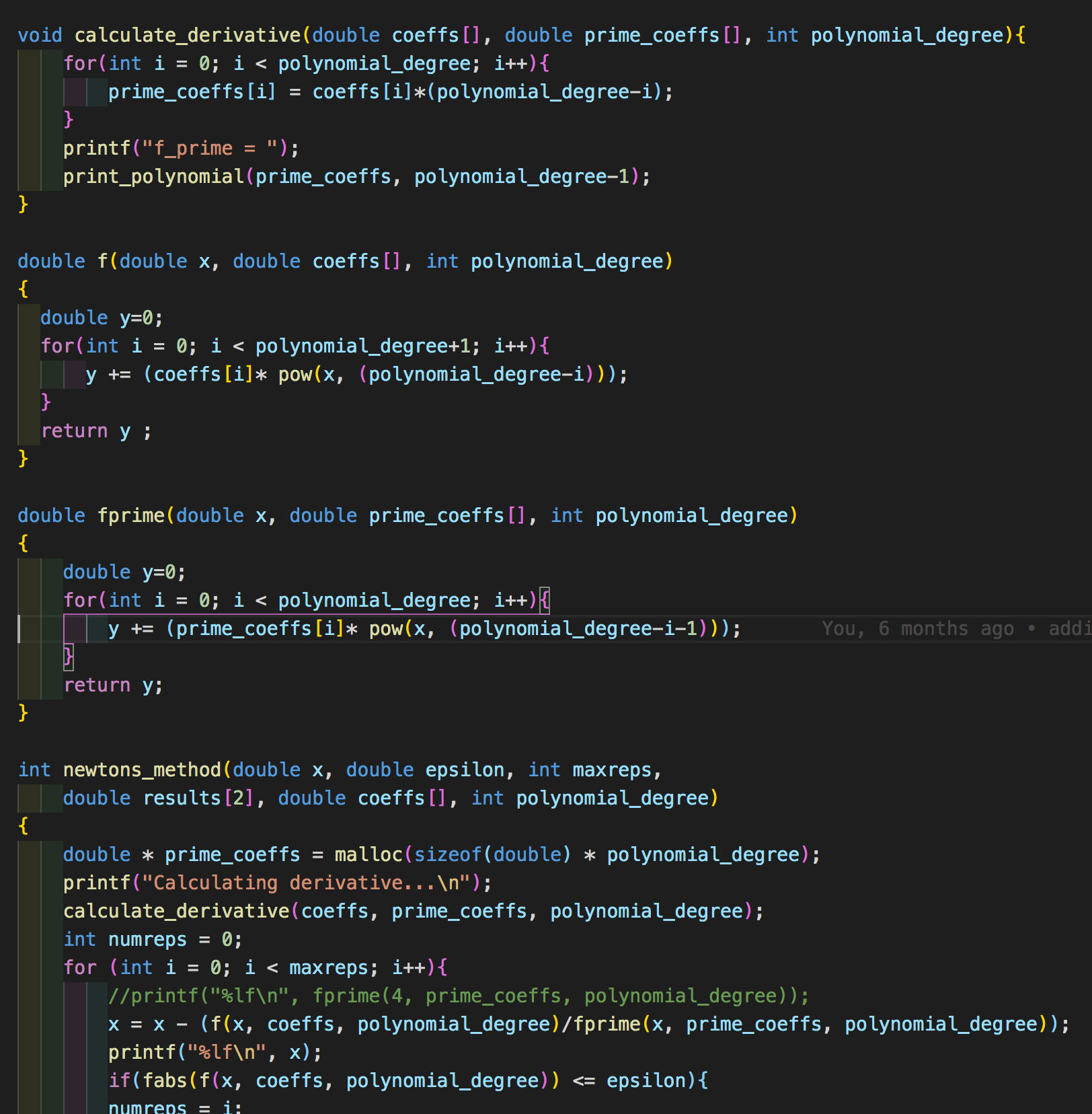
These were several projects concerned with comparing methods for finding the roots of cubic polynomials. The two main parts of this project compared fixed-point iteration with Newton's method for finding cubic roots. Interval Bisection is a related idea which is also concerned with finding roots of continuous functions when the sign of the function changes.

Natural and Cubic Splines

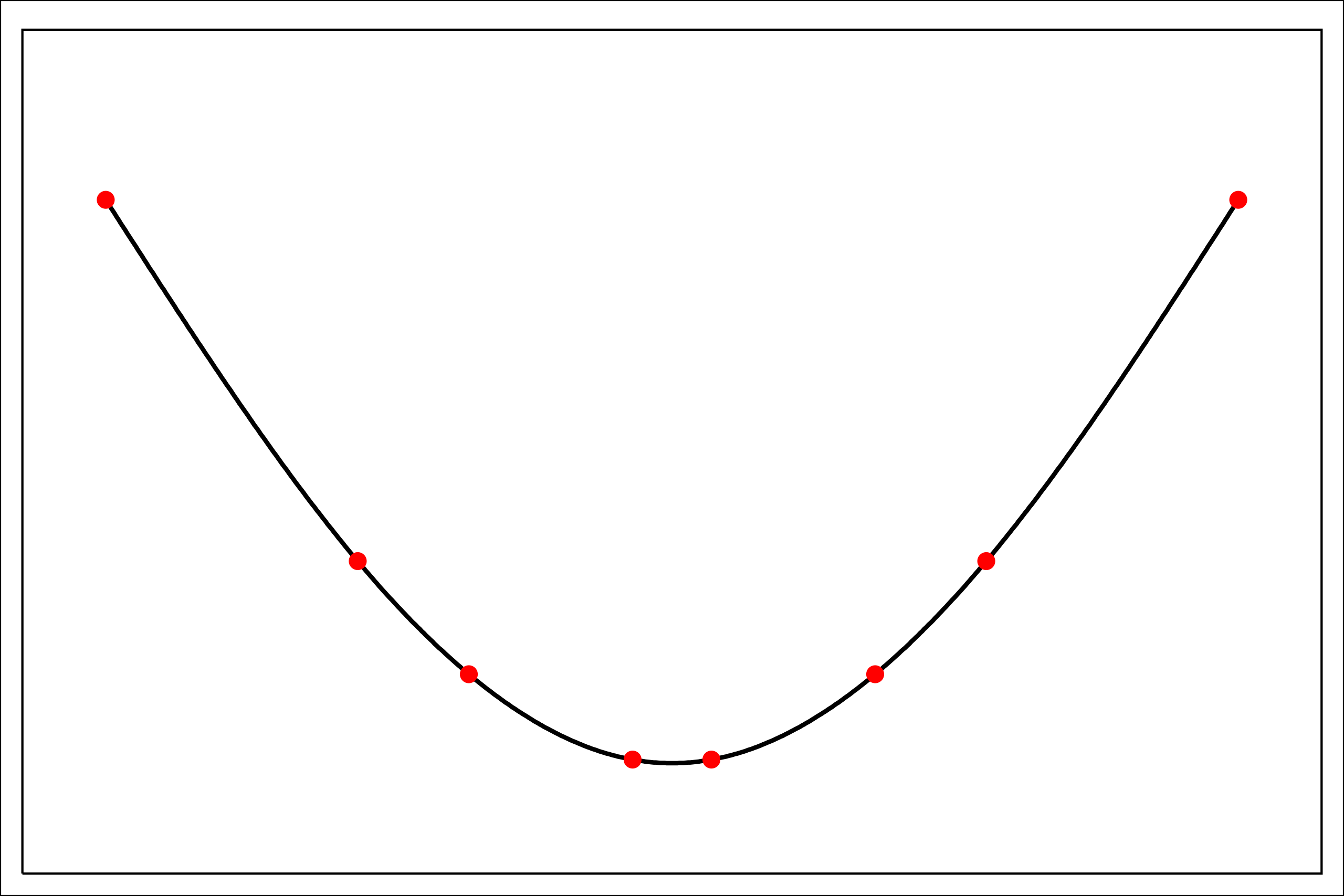
This project was the first of three projects related to polynomial interpolation. The simplest of the three, this project calculates natural splines using gaussian elimination and other techniques. Each of these projects allows the user to click points on a graphical interface before deciding to plot the polynomial.

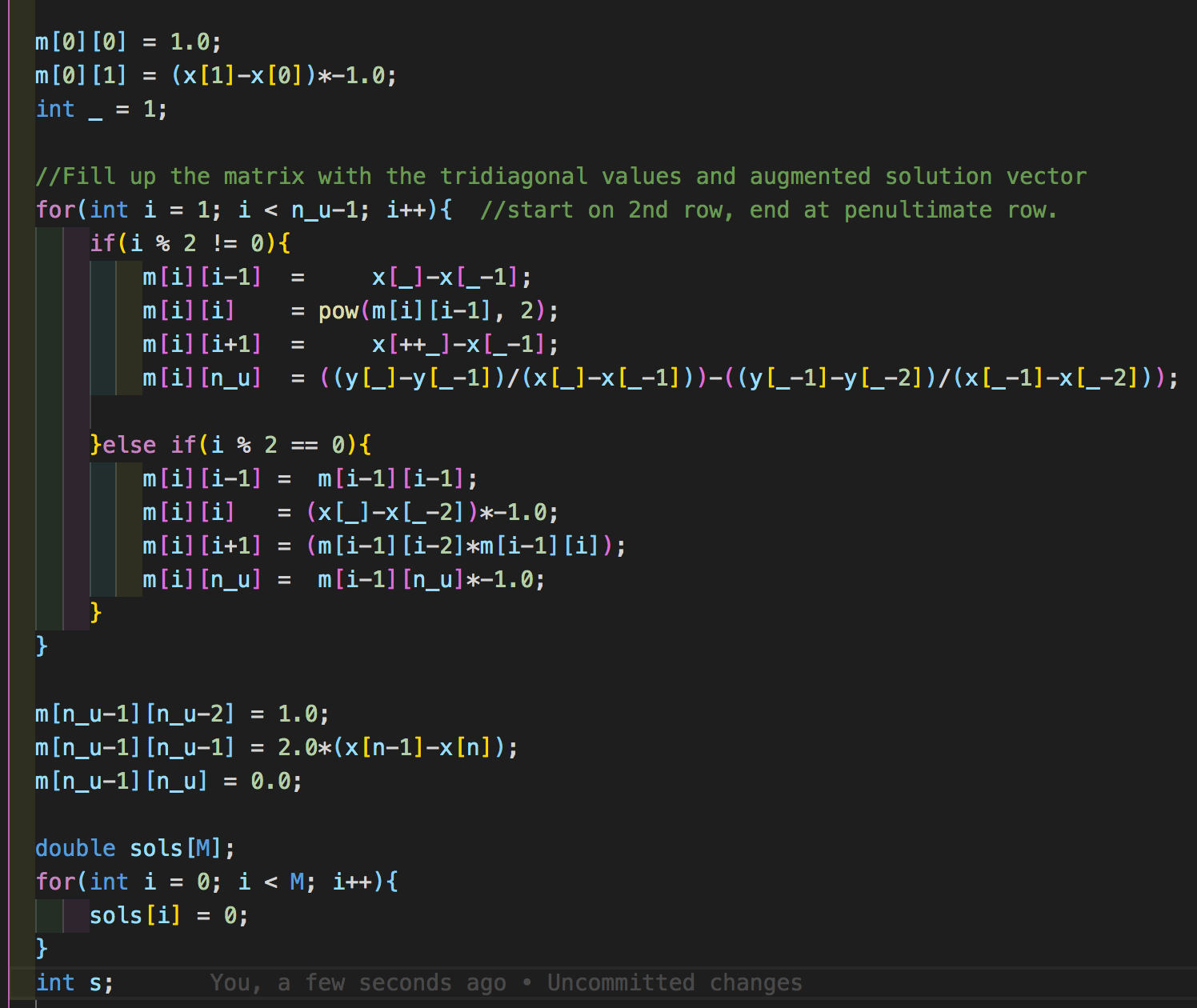
B-Splines

This project uses parameterization to calculate B-splines based on user input.

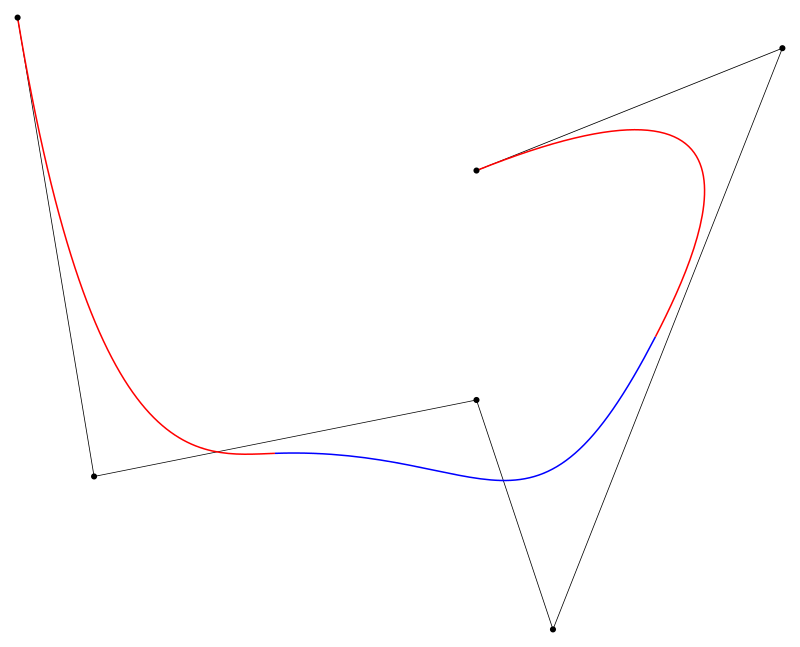
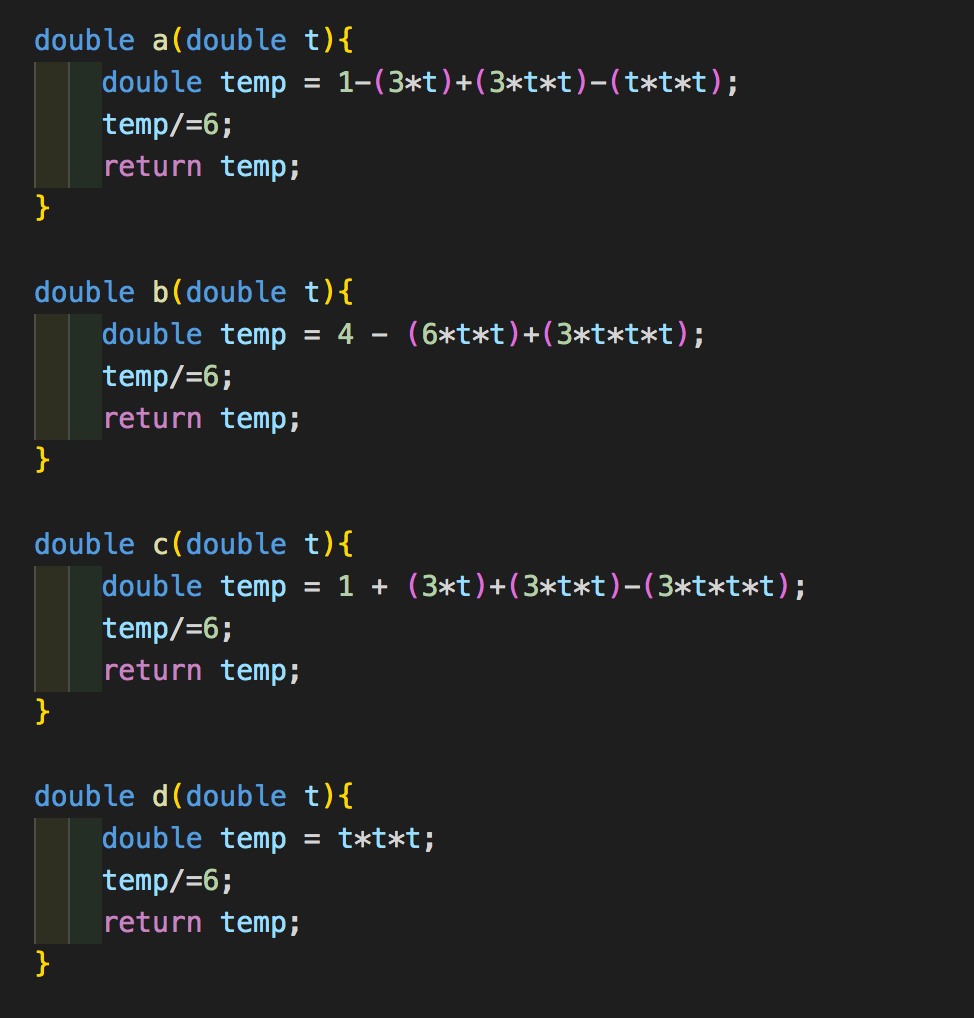
Best Polynomial Fitter

This project is similar to the above projects but this time the user is allowed to enter the desired degree of the interpolating polynomial in addition to the number and placement of points on the GUI.